[TOC]
题目来源 :LeetCode 热题 100 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台 代码来源 :刷了多遍所有题目后,参考各种题解,由本人根据自己的java编码习惯,系统化不断优化编码风格而来,整体编码风格成一个体系:比方说变量命名尽量见名知意,每道题的代码结构有相似性、注释丰富、链表题目几乎都会首先新建一个头节点、回溯模版、滑动窗口模版、dfs上下左右的技巧、二分法的技巧…好处 :利于java选手系统刷题,因为所有的代码思维是在一个空间内的,你一看就知道是一个人写的,零散地看每个题目不同人写的题解,风格往往差异很多,新手理解起来会走弯路。
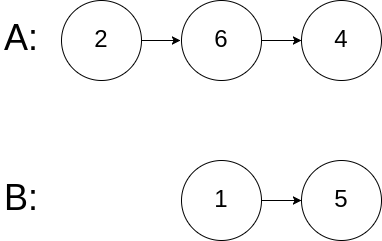
链表 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意 ,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0listA - 第一个链表listB - 第二个链表skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
1 2 3 4 5 6 输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at '8' 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。 — 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
1 2 3 4 5 输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Intersected at '2' 解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。 在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
1 2 3 4 5 输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 mlistB 中节点数目为 n1 <= m, n <= 3 * 1041 <= Node.val <= 1050 <= skipA <= m0 <= skipB <= n如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public class Solution { public ListNode getIntersectionNode (ListNode headA, ListNode headB) { if (headA == null || headB == null ) return null ; ListNode tempA = headA; ListNode tempB = headB; while (tempA != tempB) { tempA = tempA == null ? headB : tempA.next; tempB = tempB == null ? headA : tempB.next; } return tempA; } }
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
1 2 输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
示例 2:
1 2 输入:head = [1,2] 输出:[2,1]
示例 3:
提示:
链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { public ListNode reverseList (ListNode head) { if (head == null || head.next == null ) return head; ListNode newHead = head; head = head.next; newHead.next = null ; while (head != null ) { ListNode temp = head; head = head.next; temp.next = newHead; newHead = temp; } return newHead; } }
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
示例 1:
1 2 输入:head = [1,2,2,1] 输出:true
示例 2:
1 2 输入:head = [1,2] 输出:false
提示:
链表中节点数目在范围[1, 105] 内
0 <= Node.val <= 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class Solution { public boolean isPalindrome (ListNode head) { ListNode slow = head; ListNode fast = head; while (fast != null && fast.next != null && fast.next.next != null ) { slow = slow.next; fast = fast.next; fast = fast.next; } slow.next = reverse(slow.next); slow = slow.next; while (slow != null ) { if (slow.val != head.val) { return false ; } slow = slow.next; head = head.next; } return true ; } private ListNode reverse (ListNode head) { ListNode pre = null ; while (head != null ) { ListNode temp = head; head = head.next; temp.next = pre; pre = temp; } return pre; } }
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
1 2 3 输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。
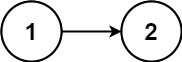
示例 2:
1 2 3 输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
1 2 3 输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
提示:
链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105pos 为 -1 或者链表中的一个 有效索引 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class Solution { public boolean hasCycle (ListNode head) { if (head == null || head.next == null ) return false ; ListNode newHead = new ListNode (0 , head); ListNode slow = newHead.next; ListNode fast = newHead.next.next; while (fast != slow) { slow = slow.next; fast = fast.next; if (fast == null ) return false ; fast = fast.next; if (fast == null ) return false ; } return true ; } }
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始 )。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递 ,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
1 2 3 输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
1 2 3 输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
1 2 3 输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105pos 的值为 -1 或者链表中的一个有效索引
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public class Solution { public ListNode detectCycle (ListNode head) { if (head == null || head.next == null ) return null ; ListNode newHead = new ListNode (0 , head); ListNode slow = newHead.next; ListNode fast = newHead.next.next; while (slow != fast) { slow = slow.next; fast = fast.next; if (fast == null ) return null ; fast = fast.next; if (fast == null ) return null ; } fast = newHead; while (slow != fast) { slow = slow.next; fast = fast.next; } return fast; } }
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
1 2 输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
示例 2:
1 2 输入:l1 = [], l2 = [] 输出:[]
示例 3:
1 2 输入:l1 = [], l2 = [0] 输出:[0]
提示:
两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100l1 和 l2 均按 非递减顺序 排列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public ListNode mergeTwoLists (ListNode list1, ListNode list2) { if (list1 == null ) return list2; if (list2 == null ) return list1; if (list1.val < list2.val) { list1.next = mergeTwoLists(list1.next, list2); return list1; } else { list2.next = mergeTwoLists(list1, list2.next); return list2; } } }
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
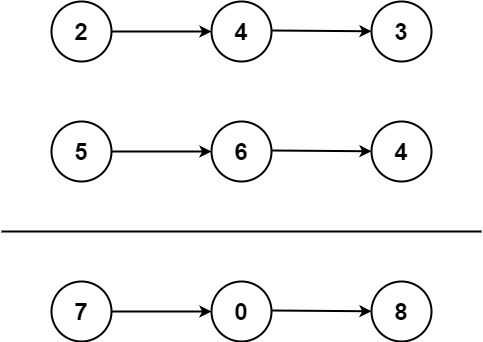
1 2 3 输入:l1 = [2,4,3], l2 = [5,6,4] 输出:[7,0,8] 解释:342 + 465 = 807.
示例 2:
1 2 输入:l1 = [0], l2 = [0] 输出:[0]
示例 3:
1 2 输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出:[8,9,9,9,0,0,0,1]
提示:
每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9题目数据保证列表表示的数字不含前导零
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 class Solution { public ListNode addTwoNumbers (ListNode l1, ListNode l2) { if (l1 == null ) return l2; if (l2 == null ) { ListNode templ1 = l1; while (l1.val >= 10 ) { if (l1.next == null ) { l1.next = new ListNode (1 ); } else { l1.next.val++; } l1.val -= 10 ; l1 = l1.next; } return templ1; } l1.val = l1.val + l2.val; if (l1.val >= 10 ) { if (l1.next == null ) { l1.next = new ListNode (1 ); } else { l1.next.val++; } l1.val -= 10 ; } l1.next = addTwoNumbers(l1.next, l2.next); return l1; } }
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
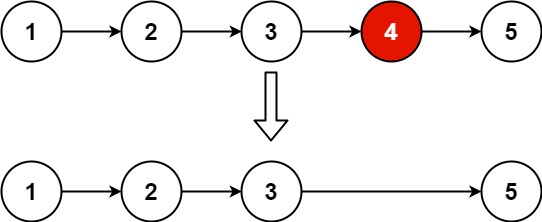
1 2 输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
1 2 输入:head = [1], n = 1 输出:[]
示例 3:
1 2 输入:head = [1,2], n = 1 输出:[1]
提示:
链表中结点的数目为 sz
1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { public ListNode removeNthFromEnd (ListNode head, int n) { ListNode newHead = new ListNode (); newHead.next = head; ListNode first = newHead; ListNode second = newHead; while (n-- > 0 ) { second = second.next; } while (second.next != null ) { second = second.next; first = first.next; } first.next = first.next.next; return newHead.next; } }
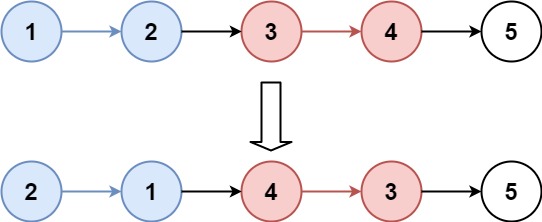
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
1 2 输入:head = [1,2,3,4] 输出:[2,1,4,3]
示例 2:
示例 3:
提示:
链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution { public ListNode swapPairs (ListNode head) { if (head == null || head.next == null ) return head; ListNode first = head; head = head.next; first.next = null ; ListNode second = head; head = head.next; second.next = null ; second.next = first; first.next = swapPairs(head); return second; } }
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
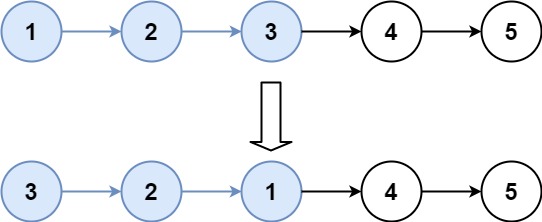
1 2 输入:head = [1,2,3,4,5], k = 2 输出:[2,1,4,3,5]
示例 2:
1 2 输入:head = [1,2,3,4,5], k = 3 输出:[3,2,1,4,5]
提示:
链表中的节点数目为 n
1 <= k <= n <= 50000 <= Node.val <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class Solution { public ListNode reverseKGroup (ListNode head, int k) { if (head == null || k == 1 ) return head; ListNode newHead = new ListNode (); ListNode tail = newHead; ListNode left = head; while (left != null ) { ListNode tempHead = new ListNode (0 , left); ListNode slow = tempHead; ListNode fast = tempHead; int count = 0 ; while (count < k) { fast = fast.next; if (fast == null ) break ; count++; } if (count < k) break ; left = fast.next; fast.next = null ; tail.next = reverse(slow.next); tail = slow.next; tail.next = null ; } tail.next = left; return newHead.next; } private ListNode reverse (ListNode head) { ListNode newHead = head; head = head.next; newHead.next = null ; while (head != null ) { ListNode tempHead = head; head = head.next; tempHead.next = newHead; newHead = tempHead; } return newHead; } }
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝 。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。 复制链表中的指针都不应指向原链表中的节点
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:
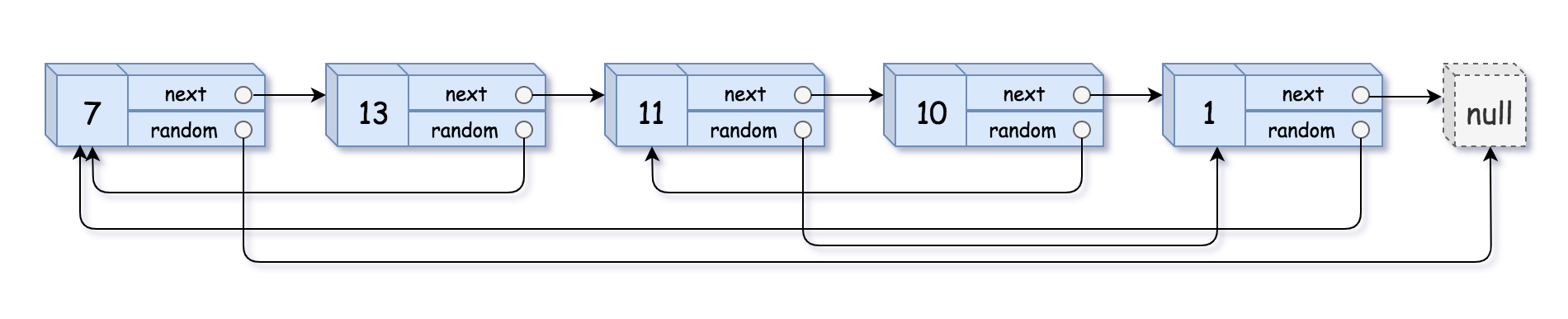
1 2 输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
1 2 输入:head = [[1,1],[2,1]] 输出:[[1,1],[2,1]]
示例 3:
1 2 输入:head = [[3,null],[3,0],[3,null]] 输出:[[3,null],[3,0],[3,null]]
提示:
0 <= n <= 1000-104 <= Node.val <= 104Node.random 为 null 或指向链表中的节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public Node copyRandomList (Node head) { if (head == null ) return null ; HashMap<Node, Node> hashMap = new HashMap <>(); Node tempHead = head; while (tempHead != null ) { hashMap.put(tempHead, new Node (tempHead.val)); tempHead = tempHead.next; } tempHead = head; while (tempHead != null ) { hashMap.get(tempHead).next = hashMap.get(tempHead.next); hashMap.get(tempHead).random = hashMap.get(tempHead.random); tempHead = tempHead.next; } return hashMap.get(head); } }
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
1 2 输入:head = [4,2,1,3] 输出:[1,2,3,4]
示例 2:
1 2 输入:head = [-1,5,3,4,0] 输出:[-1,0,3,4,5]
示例 3:
提示:
链表中节点的数目在范围 [0, 5 * 104] 内
-105 <= Node.val <= 105
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 class Solution { public ListNode sortList (ListNode head) { if (head == null || head.next == null ) return head; ListNode left = head; ListNode middleNode = getMiddle(left); ListNode right = middleNode.next; middleNode.next = null ; left = sortList(left); right = sortList(right); ListNode result = merge(left, right); return result; } private ListNode getMiddle (ListNode head) { if (head == null || head.next == null ) return head; ListNode newHead = new ListNode (-1 , head); ListNode slow = newHead.next; ListNode fast = newHead.next.next; while (fast.next != null ) { slow = slow.next; fast = fast.next; if (fast.next == null ) break ; fast = fast.next; } return slow; } private ListNode merge (ListNode l1, ListNode l2) { ListNode tempHead = new ListNode (); ListNode tail = tempHead; while (l1 != null && l2 != null ) { if (l1.val < l2.val) { tail.next = l1; l1 = l1.next; } else { tail.next = l2; l2 = l2.next; } tail = tail.next; } tail.next = l1 == null ? l2 : l1; return tempHead.next; } }
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
1 2 3 4 5 6 7 8 9 10 输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6
示例 2:
示例 3:
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i] 按 升序 排列lists[i].length 的总和不超过 10^4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class Solution { public ListNode mergeKLists (ListNode[] lists) { if (lists == null || lists.length < 1 ) return null ; ListNode newHead = new ListNode (); ListNode tail = newHead; int count = 0 ; for (ListNode list : lists) { if (list != null ) count++; } while (count > 0 ) { ListNode tempNode = new ListNode (Integer.MAX_VALUE); int tempIndex = -1 ; for (int i = 0 ; i < lists.length; i++) { ListNode tempList = lists[i]; if (tempList == null ) continue ; if (tempList.val < tempNode.val) { tempNode = tempList; tempIndex = i; } } tail.next = tempNode; lists[tempIndex] = lists[tempIndex].next; if (lists[tempIndex] == null ) { count--; } tail = tail.next; tail.next = null ; } return newHead.next; } }
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 输入 ["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"] [[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]] 输出 [null, null, null, 1, null, -1, null, -1, 3, 4] 解释 LRUCache lRUCache = new LRUCache(2); lRUCache.put(1, 1); // 缓存是 {1=1} lRUCache.put(2, 2); // 缓存是 {1=1, 2=2} lRUCache.get(1); // 返回 1 lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3} lRUCache.get(2); // 返回 -1 (未找到) lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3} lRUCache.get(1); // 返回 -1 (未找到) lRUCache.get(3); // 返回 3 lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 30000 <= key <= 100000 <= value <= 105最多调用 2 * 105 次 get 和 put
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 import java.util.HashMap;class LRUCache { private HashMap<Integer, LinkNode> cache = new HashMap <>(); private LinkNode head; private LinkNode tail; private int size; private int capacity; public LRUCache (int capacity) { this .size = 0 ; this .capacity = capacity; this .head = new LinkNode (); this .tail = new LinkNode (); this .head.next = tail; this .tail.pre = head; } public int get (int key) { LinkNode node = this .cache.get(key); if (node == null ) { return -1 ; } moveToHead(node); return node.value; } public void put (int key, int value) { LinkNode node = this .cache.get(key); if (node == null ) { node = new LinkNode (key, value); this .cache.put(key, node); addToHead(node); ++size; if (size > capacity) { LinkNode temp = removeTail(); cache.remove(temp.key); --size; } } else { node.value = value; moveToHead(node); } } private LinkNode removeTail () { LinkNode node = this .tail.pre; removeNode(node); return node; } private void removeNode (LinkNode node) { node.pre.next = node.next; node.next.pre = node.pre; } private void addToHead (LinkNode node) { node.next = this .head.next; node.pre = this .head; this .head.next.pre = node; this .head.next = node; } private void moveToHead (LinkNode node) { removeNode(node); addToHead(node); } class LinkNode { int key; int value; LinkNode pre; LinkNode next; public LinkNode () {} public LinkNode (int key, int value) { this .key = key; this .value = value; } } }
技巧 给定一个包含n + 1个整数的数组 nums ,其数字都在[1, n]范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设nums只有 一个重复的整数 ,返回这个重复的数 。
你设计的解决方案必须 不修改数组nums且只用常量级O(1)的额外空间。
示例 1:
输入: nums = [1,3,4,2,2]
输出: 2
示例 2:
输入: nums = [3,1,3,4,2]
输出: 3
示例 3 :
输入: nums = [3,3,3,3,3]
输出: 3
提示:
1 <= n <= 105nums.length == n + 11 <= nums[i] <= nnums 中只有一个整数出现两次或多次,其余整数均只出现一次
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import java.util.Arrays;class Solution { public int findDuplicate (int [] nums) { int slow = nums[0 ]; int fast = nums[slow]; while (slow != fast) { slow = nums[slow]; fast = nums[fast]; fast = nums[fast]; } fast = 0 ; while (slow != fast) { slow = nums[slow]; fast = nums[fast]; } return fast; } }
往循环链表联想
根据访问熟悉顺序可以发现,这个访问顺序是一条循环链表,且这条循环链表循环的部分第一个节点,即是我们要找的重复的数
慢指针一开始就放在第一个真正节点,算作走了一步,快指针一开始就放在第二个真正节点,算作走了两步,然后快慢指针按照自己的节奏走 那么找到循环链表的循环部分的第一个节点的步骤:
快慢指针确认有环(这道题必定有环)
将快指针放到头结点(不要放在第一个真正节点了,这样做代表多走了一步) ,慢指针不动放在上一步确认有环的停留位置
快慢指针皆一步一步走,相同即为所求点
给定一个包含红色、白色和蓝色、共n个元素的数组nums,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数0、1和2分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入: nums = [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]
示例 2:
输入: nums = [2,0,1]
输出: [0,1,2]
提示:
n == nums.length1 <= n <= 300nums[i] 为 0、1 或 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import java.util.Arrays;class Solution { public void sortColors (int [] nums) { int [] data = new int [3 ]; Arrays.stream(nums).forEach(num -> {data[num]++;}); int index = 0 ; for (int i = 0 ; i < 3 ; i++) { for (int j = 0 ; j < data[i]; j++) { nums[index++] = i; } } } }
学习下stream流简便写法吧
整数数组的一个排列 就是将其所有成员以序列或线性顺序排列。
例如,arr =[1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组nums,找出nums的下一个排列。
必须原地算法 修改,只允许使用额外常数空间。
示例 1:
输入: nums = [1,2,3]
输出: [1,3,2]
示例 2:
输入: nums = [3,2,1]
输出: [1,2,3]
示例 3:
输入: nums = [1,1,5]
输出: [1,5,1]
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public void nextPermutation (int [] nums) { if (nums == null || nums.length == 1 ) return ; int position = -1 ; for (int i = nums.length - 2 ; i >= 0 ; i--) { if (nums[i] < nums[i+1 ]) { position = i; break ; } } if (position == -1 ) { Arrays.sort(nums); return ; } for (int i = nums.length - 1 ; i > position; i--) { if (nums[i] > nums[position]) { int temp = nums[i]; nums[i] = nums[position]; nums[position] = temp; break ; } } Arrays.sort(nums, position + 1 , nums.length); } }
核心的思路就是:下一个排列,意味着尽量在尾部找更好,找到该变换的位置,接着找到这个位置代表的数往后面第一个大的数交换,随后排序这个位置往后的部分即可以达到题目所求。
第一步从尾部往前找到第一个 升序 相邻对
有这样的升序 相邻对,意味着,这样才能通过变化,找到更大的数,如果找不到,就说明就是个降序数,下一个排列就是从小到大
第一个 :因为我们找的是下一个排列,所以越靠近尾部越好相邻对 :因为判断相邻就能表示尾部可以变化来达到题意,至于到底交换哪个更大的数,到第二步去完成。
第二步找到尾部第一个大于nums[position]的数,从尾部往前循环第一个大的数就是,这是因为在第一步找的就是第一个 升序相邻对,这个标准意味着,从尾部往前循环的话,不会出现这个第一个大的数在中间的情况。
第三步 只需要排序 剩余的尾部,达到下一个排序的要求
给你一个非空 整数数组nums,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入: nums = [2,2,1]
输出: 1
示例 2 :
输入: nums = [4,1,2,1,2]
输出: 4
示例 3 :
输入: nums = [1]
输出: 1
提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104除了某个元素只出现一次以外,其余每个元素均出现两次。
1 2 3 4 5 6 7 class Solution { public int singleNumber (int [] nums) { int result = 0 ; for (int num : nums) result ^= num; return result; } }
给定一个大小为n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊n/2⌋的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入: nums = [3,2,3]
输出: 3示例 2:
输入: nums = [2,2,1,1,1,2,2]
输出: 2
提示:
n == nums.length1 <= n <= 5 * 104109 <= nums[i] <= 109
hashMap解法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import java.util.HashMap;class Solution { public int majorityElement (int [] nums) { HashMap<Integer, Integer> hashMap = new HashMap <>(); for (int i = 0 ; i < nums.length; i++) { if (hashMap.containsKey(nums[i])) { hashMap.put(nums[i], hashMap.get(nums[i]) + 1 ); if (hashMap.get(nums[i]) > nums.length / 2 ) { return nums[i]; } } else { hashMap.put(nums[i], 1 ); } } return nums[0 ]; } }
进阶:摩尔投票解法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int majorityElement (int [] nums) { int mayNum = 0 , votes = 0 ; for (int num : nums) { if (votes == 0 ) mayNum = num; votes += (num == mayNum ? 1 : -1 ); } return mayNum; } }
多维动态规划 一个机器人位于一个m x n网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入: m = 3, n = 7
输出: 28
示例 2:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下
示例 3:
输入: m = 7, n = 3
输出: 28
示例 4:
输入: m = 3, n = 3
输出: 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution { public int uniquePaths (int m, int n) { int rows = m; int cols = n; int [][] dp = new int [rows][cols]; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (row == 0 || col == 0 ) { dp[row][col] = 1 ; } else { dp[row][col] = dp[row-1 ][col] + dp[row][col-1 ]; } } } return dp[m-1 ][n-1 ]; } }
给定一个包含非负整数的 mxn 网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明: 每次只能向下或者向右移动一步。
示例 1:
输入: grid = [[1,3,1],[1,5,1],[4,2,1]]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入: grid = [[1,2,3],[4,5,6]]
输出: 12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 200
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { public int minPathSum (int [][] grid) { int rows = grid.length; int cols = grid[0 ].length; int [][] dp = new int [rows][cols]; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (row == 0 && col == 0 ) { dp[row][col] = grid[row][col]; } else if (row == 0 || col == 0 ) { if (row == 0 ) { dp[row][col] = dp[row][col-1 ] + grid[row][col]; } else { dp[row][col] = dp[row-1 ][col] + grid[row][col]; } } else { dp[row][col] = Math.min(dp[row-1 ][col], dp[row][col-1 ]); dp[row][col] += grid[row][col]; } } } return dp[rows-1 ][cols-1 ]; } }
给你一个字符串 s,找到 s 中最长的 回文子串。
示例 1:
输入: s = “babad”
输出: “bab”
解释: “aba” 同样是符合题意的答案。
示例 2:
输入: s = “cbbd”
输出: “bb”
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母组成
中心扩散解法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public String longestPalindrome (String s) { String result = "" ; for (int i = 0 ; i < s.length(); i++) { String tempResult = get(s, i, i); if (i < s.length() - 1 && s.charAt(i) == s.charAt(i+1 )) { String tempResult1 = get(s, i, i + 1 ); tempResult = tempResult.length() > tempResult1.length() ? tempResult : tempResult1; } if (tempResult.length() > result.length()) { result = tempResult; } } return result; } private String get (String s, int left, int right) { while (left - 1 >= 0 && right + 1 < s.length()) { if (s.charAt(left - 1 ) != s.charAt(right + 1 )) { break ; } left--; right++; } return s.substring(left, right + 1 ); } }
dp解法 学习下动态规划解决方法
boolean dp[l][r] 表示字符串从 i 到 j 这段是否为回文。试想如果 dp[l][r]=true,我们要判断 dp[l-1][r+1] 是否为回文。只需要判断字符串在(l-1)和(r+1)两个位置是否为相同的字符
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 public String longestPalindrome (String s) { if (s == null || s.length() < 2 ) { return s; } int strLen = s.length(); int maxStart = 0 ; int maxEnd = 0 ; int maxLen = 1 ; boolean [][] dp = new boolean [strLen][strLen]; for (int r = 1 ; r < strLen; r++) { for (int l = 0 ; l < r; l++) { if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1 ][r - 1 ])) { dp[l][r] = true ; if (r - l + 1 > maxLen) { maxLen = r - l + 1 ; maxStart = l; maxEnd = r; } } } } return s.substring(maxStart, maxEnd + 1 ); }
给定两个字符串text1和text2,返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列,返回 0 。
一个字符串的子序列是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,”ace” 是”abcde”的子序列,但 “aec” 不是”abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。
示例 1:
输入: text1 = “abcde”, text2 = “ace”
输出: 3
解释: 最长公共子序列是 “ace” ,它的长度为 3 。
示例 2:
输入: text1 = “abc”, text2 = “abc”
输出: 3
解释: 最长公共子序列是 “abc” ,它的长度为 3 。
示例 3:
输入: text1 = “abc”, text2 = “def”
输出: 0
解释: 两个字符串没有公共子序列,返回 0 。
提示:
1 <= text1.length, text2.length <= 1000text1 和 text2 仅由小写英文字符组成。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { public int longestCommonSubsequence (String text1, String text2) { int [][] dp = new int [text1.length() + 1 ][text2.length() + 1 ]; for (int i = 1 ; i <= text1.length(); i++) { for (int j = 1 ; j <= text2.length(); j++) { if (text1.charAt(i-1 ) == text2.charAt(j-1 )) { dp[i][j] = dp[i-1 ][j-1 ] + 1 ; } else { dp[i][j] = Math.max(dp[i-1 ][j], dp[i][j-1 ]); } } } return dp[text1.length()][text2.length()]; } }
给你两个单词word1和 word2, 请返回将 word1转换成word2所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
示例 1:
输入: word1 = “horse”, word2 = “ros”
输出: 3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入: word1 = “intention”, word2 = “execution”
输出: 5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
提示:
0 <= word1.length, word2.length <= 500word1 和 word2 由小写英文字母组成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public int minDistance (String word1, String word2) { int m = word1.length(); int n = word2.length(); int [][] dp = new int [m + 1 ][n + 1 ]; for (int i = 0 ; i <= m; i++) { for (int j = 0 ; j <= n; j++) { if (i == 0 ) { dp[i][j] = j; } else if (j == 0 ) { dp[i][j] = i; } else { int changeFlag = word1.charAt(i-1 ) == word2.charAt(j-1 ) ? 0 : 1 ; dp[i][j] = Math.min(dp[i-1 ][j-1 ] + changeFlag, Math.min(dp[i-1 ][j] + 1 , dp[i][j-1 ] + 1 )); } } } return dp[m][n]; } }
动态规划 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
1 2 3 4 5 输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
1 2 3 4 5 6 输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public int climbStairs (int n) { if (n <= 2 ) return n; int [] dp = new int [n+1 ]; dp[0 ] = 0 ; dp[1 ] = 1 ; dp[2 ] = 2 ; for (int i = 3 ; i <= n; i++) { dp[i] = dp[i-1 ] + dp[i-2 ]; } return dp[n]; } }
给定一个非负整数 numRows,numRows
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
1 2 输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
1 2 输入: numRows = 1 输出: [[1]]
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public List<List<Integer>> generate (int numRows) { List<List<Integer>> result = new ArrayList <>(); result.add(List.of(1 )); if (numRows == 1 ) return result; result.add(List.of(1 , 1 )); if (numRows == 2 ) return result; for (int i = 3 ; i <= numRows; i++) { List<Integer> pre = result.get(i - 2 ); List<Integer> newList = new ArrayList <>(); for (int j = 0 ; j < i; j++) { if (j == 0 || j == i-1 ) { newList.add(1 ); } else { newList.add(pre.get(j-1 ) + pre.get(j)); } } result.add(newList); } return result; } }
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
1 2 3 4 输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
1 2 3 4 输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int rob (int [] nums) { int [] dp = new int [nums.length]; for (int i = 0 ; i < nums.length; i++) { if (i == 0 ) { dp[i] = nums[i]; } else if (i == 1 ) { dp[i] = Math.max(nums[0 ], nums[1 ]); } else { dp[i] = Math.max(dp[i-1 ], dp[i-2 ] + nums[i]); } } return dp[nums.length - 1 ]; } }
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
1 2 3 输入:n = 12 输出:3 解释:12 = 4 + 4 + 4
示例 2:
1 2 3 输入:n = 13 输出:2 解释:13 = 4 + 9
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public int numSquares (int n) { if (n == 0 ) return 0 ; int [] dp = new int [n+1 ]; for (int num = 1 ; num <= n; num++) { dp[num] = num; for (int j = 1 ; j * j <= num; j++) { dp[num] = Math.min(dp[num], dp[num - j*j] + 1 ); } } return dp[n]; } }
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
1 2 3 输入:coins = [1, 2, 5], amount = 11 输出:3 解释:11 = 5 + 5 + 1
示例 2:
1 2 输入:coins = [2], amount = 3 输出:-1
示例 3:
1 2 输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import java.util.Arrays;class Solution { public int coinChange (int [] coins, int amount) { if (coins == null || coins.length < 1 ) { return -1 ; } int [] dp = new int [amount + 1 ]; Arrays.fill(dp, amount + 1 ); dp[0 ] = 0 ; for (int i = 1 ; i <= amount; i++) { for (int coin : coins) { if (i >= coin) { dp[i] = Math.min(dp[i], dp[i-coin] + 1 ); } } } return dp[amount] == amount + 1 ? -1 : dp[amount]; } }
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意: 不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
1 2 3 输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true 解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
1 2 3 4 输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true 解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。 注意,你可以重复使用字典中的单词。
示例 3:
1 2 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] 输出: false
提示:
1 <= s.length <= 3001 <= wordDict.length <= 10001 <= wordDict[i].length <= 20s 和 wordDict[i] 仅由小写英文字母组成wordDict 中的所有字符串 互不相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public boolean wordBreak (String s, List<String> wordDict) { boolean [] dp = new boolean [s.length() + 1 ]; dp[0 ] = true ; for (int i = 1 ; i <= s.length(); i++) { for (String word : wordDict) { if (i >= word.length() && s.substring(i - word.length(), i).equals(word)) { if (dp[i-word.length()]) { dp[i] = true ; } } } } return dp[s.length()]; } }
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
1 2 3 输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
1 2 输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
1 2 输入:nums = [7,7,7,7,7,7,7] 输出:1
提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution { public int lengthOfLIS (int [] nums) { if (nums.length == 1 ) { return 1 ; } int [] dp = new int [nums.length]; Arrays.fill(dp, 1 ); int max = 0 ; for (int i = 0 ; i < nums.length; i++) { for (int j = 0 ; j < i; j++) { if (nums[j] < nums[i]) { dp[i] = Math.max(dp[i], dp[j] + 1 ); } max = Math.max(max, dp[i]); } } return max; } }
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
1 2 3 输入: nums = [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
1 2 3 输入: nums = [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104-10 <= nums[i] <= 10nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public int maxProduct (int [] nums) { int result = nums[0 ]; int positiveMax = nums[0 ]; int negativeMin = nums[0 ]; for (int i = 1 ; i < nums.length; i++) { if (nums[i] < 0 ) { int temp = positiveMax; positiveMax = negativeMin; negativeMin = temp; } positiveMax = Math.max(nums[i], positiveMax*nums[i]); negativeMin = Math.min(nums[i], negativeMin*nums[i]); result = Math.max(result, positiveMax); } return result; } }
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
1 2 3 输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
1 2 3 输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import java.util.Arrays;class Solution { public boolean canPartition (int [] nums) { int sum = Arrays.stream(nums).sum(); if (sum % 2 != 0 ) { return false ; } int target = sum / 2 ; boolean [][] dp = new boolean [nums.length + 1 ][target + 1 ]; dp[0 ][0 ] = true ; for (int i = 1 ; i <= nums.length; i++) { for (int j = 0 ; j <= target; j++) { if (j < nums[i-1 ]) { dp[i][j] = dp[i-1 ][j]; } else { dp[i][j] = dp[i-1 ][j] || dp[i-1 ][j - nums[i-1 ]]; } } } return dp[nums.length][target]; } }
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
1 2 3 输入:s = "(()" 输出:2 解释:最长有效括号子串是 "()"
示例 2:
1 2 3 输入:s = ")()())" 输出:4 解释:最长有效括号子串是 "()()"
示例 3:
提示:
0 <= s.length <= 3 * 104s[i] 为 '(' 或 ')'
栈解决 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public int longestValidParentheses (String s) { int max = 0 ; Stack<Integer> stack = new Stack <>(); stack.push(-1 ); for (int i = 0 ; i < s.length(); i++) { if (s.charAt(i) == '(' ) { stack.push(i); } else { stack.pop(); if (stack.empty()) { stack.push(i); } else { max = Math.max(max, i - stack.peek()); } } } return max; } }
动态规划 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public int longestValidParentheses (String s) { int max = 0 ; s = " " + s; int dp[] = new int [s.length()]; for (int i = 2 ; i < s.length(); i++) { if (s.charAt(i) == '(' ) { dp[i] = 0 ; } else { if (s.charAt(i-1 ) == '(' ) { dp[i] = dp[i-2 ] + 2 ; } else if (s.charAt(i - dp[i-1 ] - 1 ) == '(' ) { dp[i] = dp[i-1 ] + 2 + dp[i- dp[i-1 ] - 2 ]; } } max = Math.max(max, dp[i]); } return max; } }
贪心算法 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
1 2 3 4 输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
1 2 3 输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public int maxProfit (int [] prices) { int buyMin = Integer.MIN_VALUE; int sellGet = 0 ; for (int i = 0 ; i < prices.length; i++) { buyMin = Math.max(buyMin, -prices[i]); sellGet = Math.max(sellGet, prices[i] + buyMin); } return sellGet; } }
总的来说,即是找到最小的,并且在尾部找到最大的,这样便可以实现低买高卖。
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
1 2 3 输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
1 2 3 输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 1040 <= nums[i] <= 105
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution { public boolean canJump (int [] nums) { int maxRightIndex = nums[0 ]; for (int i = 1 ; i < nums.length; i++) { if (i > maxRightIndex) { break ; } maxRightIndex = Math.max(maxRightIndex, i + nums[i]); } return maxRightIndex >= nums.length - 1 ; } }
给定一个长度为 n 的 0 索引 整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i] i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
1 2 3 4 输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
1 2 输入: nums = [2,3,0,1,4] 输出: 2
提示:
1 <= nums.length <= 1040 <= nums[i] <= 1000题目保证可以到达 nums[n-1]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public int jump (int [] nums) { int currentRightIndex = 0 ; int maxPostion = 0 ; int steps = 0 ; for (int i = 0 ; i < nums.length; i++) { if (i > currentRightIndex) { currentRightIndex = maxPostion; steps++; } maxPostion = Math.max(maxPostion, i + nums[i]); } return steps; } }
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
示例 1:
1 2 3 4 5 6 输入:s = "ababcbacadefegdehijhklij" 输出:[9,7,8] 解释: 划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的,因为划分的片段数较少。
示例 2:
1 2 输入:s = "eccbbbbdec" 输出:[10]
提示:
1 <= s.length <= 500s 仅由小写英文字母组成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { public List<Integer> partitionLabels (String s) { List<Integer> result = new ArrayList <>(); HashMap<Character, Integer> rightLocationMap = new HashMap <>(); for (int i = 0 ; i < s.length(); i++) { rightLocationMap.put(s.charAt(i), i); } int index = 0 ; while (index < s.length()) { int right = rightLocationMap.get(s.charAt(index)); for (int left = index + 1 ; left < right; left++) { right = Math.max(right, rightLocationMap.get(s.charAt(left))); } result.add(right - index + 1 ); index = right + 1 ; } return result; } }
堆 给定整数数组 nums 和整数 k,请返回数组中第 **k** 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
1 2 输入: [3,2,1,5,6,4], k = 2 输出: 5
示例 2:
1 2 输入: [3,2,3,1,2,4,5,5,6], k = 4 输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public int findKthLargest (int [] nums, int k) { int start = 0 ; int end = nums.length - 1 ; int targetIndex = nums.length - k; while (start < end) { int chooseIndex = getPartionIndex(nums, start, end); if (chooseIndex == targetIndex) { return nums[chooseIndex]; } else if (chooseIndex < targetIndex) { start = chooseIndex + 1 ; } else { end = chooseIndex - 1 ; } } return nums[start]; } private int getPartionIndex (int [] nums, int left, int right) { int key = nums[left]; while (left < right) { while (left < right && nums[right] >= key) { right--; } nums[left] = nums[right]; while (left < right && nums[left] < key) { left++; } nums[right] = nums[left]; } nums[left] = key; return left; } }
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
1 2 输入: nums = [1,1,1,2,2,3], k = 2 输出: [1,2]
示例 2:
1 2 输入: nums = [1], k = 1 输出: [1]
提示:
1 <= nums.length <= 105k 的取值范围是 [1, 数组中不相同的元素的个数]题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 import java.util.*;import java.util.stream.Collectors;class Solution { public int [] topKFrequent(int [] nums, int k) { int [] result = new int [k]; HashMap<Integer, Node> map = new HashMap <>(); for (int i = 0 ; i < nums.length; i++) { if (!map.containsKey(nums[i])) { map.put(nums[i], new Node (nums[i], 1 )); } else { Node temp = map.get(nums[i]); temp.count++; } } List<Node> nodeList = map.values().stream().collect(Collectors.toList()); Collections.sort(nodeList, (a, b) -> {return b.count - a.count;}); for (int i = 0 ; i < k; i++) { result[i] = nodeList.get(i).num; } return result; } class Node { public int num; public int count; public Node (int num, int count) { this .num = num; this .count = count; } } }
中位数 是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
例如 arr = [2,3,4] 的中位数是 3 。
例如 arr = [2,3] 的中位数是 (2 + 3) / 2 = 2.5 。
实现 MedianFinder 类:
MedianFinder() 初始化 MedianFinder 对象。void addNum(int num) 将数据流中的整数 num 添加到数据结构中。double findMedian() 返回到目前为止所有元素的中位数。与实际答案相差 10-5 以内的答案将被接受。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 12 13 输入 ["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"] [[], [1], [2], [], [3], []] 输出 [null, null, null, 1.5, null, 2.0] 解释 MedianFinder medianFinder = new MedianFinder(); medianFinder.addNum(1); // arr = [1] medianFinder.addNum(2); // arr = [1, 2] medianFinder.findMedian(); // 返回 1.5 ((1 + 2) / 2) medianFinder.addNum(3); // arr[1, 2, 3] medianFinder.findMedian(); // return 2.0
提示:
-105 <= num <= 105在调用 findMedian 之前,数据结构中至少有一个元素
最多 5 * 104 次调用 addNum 和 findMedian
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class MedianFinder { Queue<Integer> A, B; public MedianFinder () { A = new PriorityQueue <>((x, y) -> (y - x)); B = new PriorityQueue <>(); } public void addNum (int num) { if (A.size() != B.size()) { B.add(num); A.add(B.poll()); } else { A.add(num); B.add(A.poll()); } } public double findMedian () { return A.size() != B.size() ? B.peek() : ((A.peek() + B.peek()) / 2.0 ); } }
栈 给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
示例 2:
示例 3:
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import java.util.LinkedList;class Solution { public boolean isValid (String s) { LinkedList<Character> stack = new LinkedList <>(); for (int i = 0 ; i < s.length(); i++) { char c = s.charAt(i); if (c == '[' || c == '{' || c == '(' ) { stack.push(c); } else { if (stack.isEmpty()) return false ; char top = stack.peek(); if ((c == ']' && top == '[' ) || (c == ')' && top == '(' ) || (c == '}' && top == '{' ) ) { stack.pop(); } else { return false ; } } } return stack.isEmpty(); } }
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。int getMin() 获取堆栈中的最小元素。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]] 输出: [null,null,null,null,-3,null,0,-2] 解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top 和 getMin 操作总是在 非空栈 上调用push, pop, top, and getMin最多被调用 3 * 104 次
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 import java.util.LinkedList;class MinStack { private LinkedList<Integer> stack; private LinkedList<Integer> minStack; public MinStack () { stack = new LinkedList <>(); minStack = new LinkedList <>(); } public void push (int val) { stack.push(val); if (minStack.isEmpty() || minStack.peek() >= val) { minStack.push(val); } else { minStack.push(minStack.peek()); } } public void pop () { stack.pop(); minStack.pop(); } public int top () { return stack.peek(); } public int getMin () { return minStack.peek(); } }
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
1 2 输入:s = "3[a]2[bc]" 输出:"aaabcbc"
示例 2:
1 2 输入:s = "3[a2[c]]" 输出:"accaccacc"
示例 3:
1 2 输入:s = "2[abc]3[cd]ef" 输出:"abcabccdcdcdef"
示例 4:
1 2 输入:s = "abc3[cd]xyz" 输出:"abccdcdcdxyz"
提示:
1 <= s.length <= 30s 由小写英文字母、数字和方括号 '[]' 组成s 保证是一个 有效 的输入。s 中所有整数的取值范围为 [1, 300]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { public String decodeString (String s) { int tempNum = 0 ; StringBuilder result = new StringBuilder (); Stack<Integer> numStack = new Stack <>(); Stack<StringBuilder> resultStack = new Stack <>(); for (char c : s.toCharArray()){ if (c == '[' ){ numStack.push(tempNum); resultStack.push(result); tempNum = 0 ; result = new StringBuilder (); }else if (c ==']' ){ int curNum = numStack.pop(); StringBuilder temp = new StringBuilder (); for (int i = 0 ; i < curNum; i++){ temp.append(result); } result = resultStack.pop().append(temp); }else if (c >= '0' && c <= '9' ){ tempNum = c - '0' + tempNum * 10 ; }else { result.append(c); } } return result.toString(); } }
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
1 2 输入: temperatures = [73,74,75,71,69,72,76,73] 输出: [1,1,4,2,1,1,0,0]
示例 2:
1 2 输入: temperatures = [30,40,50,60] 输出: [1,1,1,0]
示例 3:
1 2 输入: temperatures = [30,60,90] 输出: [1,1,0]
提示:
1 <= temperatures.length <= 10530 <= temperatures[i] <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public int [] dailyTemperatures(int [] temperatures) { int [] result = new int [temperatures.length]; LinkedList<Integer> stack = new LinkedList <>(); for (int i = 0 ; i < temperatures.length; i++) { while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) { result[stack.peek()] = i - stack.poll(); } stack.push(i); } return result; } }
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
1 2 3 输入:heights = [2,1,5,6,2,3] 输出:10 解释:最大的矩形为图中红色区域,面积为 10
示例 2:
1 2 输入: heights = [2,4] 输出: 4
提示:
1 <= heights.length <=1050 <= heights[i] <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Solution { public int largestRectangleArea (int [] heights) { if (heights.length == 1 ) return heights[0 ]; int result = 0 ; LinkedList<Integer> stack = new LinkedList <>(); for (int i = 0 ; i < heights.length; i++) { while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) { int curHeight = heights[stack.poll()]; while (!stack.isEmpty() && curHeight == heights[stack.peek()]) { stack.poll(); } int curWidth = stack.isEmpty() ? i : i - stack.peek() - 1 ; result = Math.max(result, curHeight * curWidth); } stack.push(i); } while (!stack.isEmpty()) { int curHeight = heights[stack.poll()]; while (!stack.isEmpty() && curHeight == heights[stack.peek()]) { stack.poll(); } int curWidth = stack.isEmpty() ? heights.length : heights.length - stack.peek() - 1 ; result = Math.max(result, curHeight * curWidth); } return result; } }
二分查找 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
1 2 输入: nums = [1,3,5,6], target = 5 输出: 2
示例 2:
1 2 输入: nums = [1,3,5,6], target = 2 输出: 1
示例 3:
1 2 输入: nums = [1,3,5,6], target = 7 输出: 4
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums 为 无重复元素 的 升序 排列数组-104 <= target <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int searchInsert (int [] nums, int target) { int left = 0 ; int right = nums.length - 1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] == target) { return mid; } else if (nums[mid] < target) { left = mid + 1 ; } else { right = mid - 1 ; } } return left; } }
给你一个满足下述两条属性的 m x n 整数矩阵:
每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例 1:
1 2 输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
示例 2:
1 2 输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution { public boolean searchMatrix (int [][] matrix, int target) { int rows = matrix.length; int cols = matrix[0 ].length; for (int row = 0 ; row < rows; row++) { for (int col = cols - 1 ; col >= 0 ; col--) { if (matrix[row][col] == target) { return true ; } else if (matrix[row][col] < target) { break ; } else { continue ; } } } return false ; } }
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
1 2 输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]
示例 2:
1 2 输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
示例 3:
1 2 输入:nums = [], target = 0 输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums 是一个非递减数组-109 <= target <= 109
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 class Solution { public int [] searchRange(int [] nums, int target) { int [] result = {-1 , -1 }; int resultLeftIndex = -1 ; int resultRightIndex = -1 ; int left = 0 ; int right = nums.length - 1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] == target) { resultLeftIndex = mid; resultRightIndex = mid; break ; } else if (nums[mid] < target) { left = mid + 1 ; } else { right = mid - 1 ; } } if (resultLeftIndex == -1 ) return result; int tempLeft = getFromDirection(nums, 0 , resultLeftIndex - 1 , target, 1 ); int tempRight = getFromDirection(nums, resultRightIndex + 1 , nums.length - 1 , target, 2 ); if (tempLeft != -1 ) resultLeftIndex = tempLeft; if (tempRight != - 1 ) resultRightIndex = tempRight; result[0 ] = resultLeftIndex; result[1 ] = resultRightIndex; return result; } private int getFromDirection (int [] nums, int start, int end, int target, int direction) { int left = start; int right = end; int tempResult = -1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] == target) { tempResult = mid; if (direction == 1 ) right = mid - 1 ; else left = mid + 1 ; } else if (nums[mid] < target) { left = mid + 1 ; } else { right = mid - 1 ; } } return tempResult; } }
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转 ,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
1 2 输入:nums = [4,5,6,7,0,1,2], target = 0 输出:4
示例 2:
1 2 输入:nums = [4,5,6,7,0,1,2], target = 3 输出:-1
示例 3:
1 2 输入:nums = [1], target = 0 输出:-1
提示:
1 <= nums.length <= 5000-104 <= nums[i] <= 104nums 中的每个值都 独一无二 题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution { public int search (int [] nums, int target) { return search(nums, 0 , nums.length - 1 , target); } private int search (int [] nums, int left, int right, int target) { if (left > right) return -1 ; int mid = left + (right - left) / 2 ; int result = -1 ; if (nums[mid] == target) return mid; if (nums[mid] > nums[left] && nums[left] <= target && target < nums[mid]) result = binarySearch(nums, left, mid - 1 , target); else result = search(nums, mid + 1 , right, target); if (result != -1 ) return result; if (nums[mid] < nums[right] && nums[mid] < target && target <= nums[right]) result = binarySearch(nums, mid +1 , right , target); else result = search(nums, left, mid - 1 , target); return result; } private int binarySearch (int [] nums, int left, int right, int target) { if (left > right) return -1 ; int result = -1 ; while (left <= right) { int mid = left + (right - left) / 2 ; if (nums[mid] == target) { result = mid; break ; } else if (nums[mid] < target) { left = mid + 1 ; } else { right = mid - 1 ; } } return -1 ; } }
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
1 2 3 输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
1 2 3 输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
1 2 3 输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums 中的所有整数 互不相同 nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { private int min = Integer.MAX_VALUE; public int findMin (int [] nums) { int left = 0 ; int right = nums.length - 1 ; int mid = left + (right - left) / 2 ; min = nums[mid]; findMin(nums, left, mid - 1 ); findMin(nums, mid + 1 , right); return min; } private void findMin (int [] nums, int left, int right) { if (left > right) { return ; } int mid = left + (right - left) / 2 ; if (nums[mid] >= nums[left]) { min = Math.min(min, nums[left]); } findMin(nums, left, mid - 1 ); if (nums[mid] <= nums[right]) { min = Math.min(min, nums[mid]); } findMin(nums, mid + 1 , right); } }
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
1 2 3 输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
1 2 3 输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class Solution { public double findMedianSortedArrays (int [] nums1, int [] nums2) { int indexFirstK = (nums1.length + nums2.length + 1 ) / 2 ; int indexSecondK = (nums1.length + nums2.length + 2 ) / 2 ; return (getKth(nums1, 0 , nums1.length - 1 , nums2, 0 , nums2.length - 1 , indexFirstK) + getKth(nums1, 0 , nums1.length - 1 , nums2, 0 , nums2.length - 1 , indexSecondK)) * 0.5 ; } private int getKth (int [] nums1, int start1, int end1, int [] nums2, int start2, int end2, int k) { int len1 = end1 - start1 + 1 ; int len2 = end2 - start2 + 1 ; if (len1 > len2) { return getKth(nums2, start2, end2, nums1, start1, end1, k); } if (len1 == 0 ) { return nums2[start2 + k - 1 ]; } if (k == 1 ) { return Math.min(nums1[start1], nums2[start2]); } int temp1 = start1 + Math.min(len1, k / 2 ) - 1 ; int temp2 = start2 + Math.min(len2, k / 2 ) - 1 ; if (nums1[temp1] > nums2[temp2]) { return getKth(nums1, start1, end1, nums2, temp2 + 1 , end2, k - (temp2 -start2 + 1 )); } else { return getKth(nums1, temp1 + 1 , end1, nums2, start2, end2, k - (temp1- start1 + 1 )); } } }
回溯 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
1 2 输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
1 2 输入:nums = [0,1] 输出:[[0,1],[1,0]]
示例 3:
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums 中的所有整数 互不相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 import java.util.ArrayList;import java.util.Arrays;import java.util.stream.Collectors;import static java.util.stream.Collectors.toList;class Solution { List<List<Integer>> result = new ArrayList <>(); public List<List<Integer>> permute (int [] nums) { backTracking(nums, 0 ); return result; } private void backTracking (int [] nums, int startIndex) { if (startIndex == nums.length - 1 ) { List<Integer> temp = Arrays.stream(nums).boxed().collect(toList()); result.add(temp); return ; } for (int i = startIndex; i < nums.length; i++) { swap(nums, i, startIndex); backTracking(nums, startIndex + 1 ); swap(nums, i, startIndex); } } private void swap (int [] nums, int a, int b) { int temp = nums[a]; nums[a] = nums[b]; nums[b] = temp; } }
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
1 2 输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
1 2 输入:nums = [0] 输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums 中的所有元素 互不相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution { private List<List<Integer>> result = new ArrayList <>(); public List<List<Integer>> subsets (int [] nums) { List<Integer> tempList = new ArrayList <>(); backTracking(nums, 0 , tempList); return result; } private void backTracking (int [] nums, int startIndex, List<Integer> tempList) { result.add(new ArrayList <>(tempList)); if (startIndex == nums.length) return ; for (int i = startIndex; i < nums.length; i++) { tempList.add(nums[i]); backTracking(nums, i + 1 , tempList); tempList.remove(tempList.size() - 1 ); } } }
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
1 2 输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
示例 3:
1 2 输入:digits = "2" 输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i] 是范围 ['2', '9'] 的一个数字。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 import java.util.ArrayList;import java.util.HashMap;import java.util.List;class Solution { List<String> result = new ArrayList <>(); public List<String> letterCombinations (String digits) { if (digits == null || digits.length() < 1 ) return result; HashMap<Character, char []> hashMap = new HashMap <>(); char currentChar = 'a' ; for (int num = 2 ; num <= 9 ; num++) { int i = 3 ; if (num == 7 || num == 9 ) { i = 4 ; } char [] tempArray = new char [i]; for (int j = 0 ; j < i; j++) { tempArray[j] = currentChar++; } hashMap.put((char )(num + '0' ), tempArray); } List<char []> arrayList = new ArrayList <>(); for (int i = 0 ; i < digits.length(); i++) { arrayList.add(hashMap.get(digits.charAt(i))); } StringBuilder sb = new StringBuilder (); backTracking(arrayList, 0 , sb); return result; } private void backTracking (List<char []> list, int listIndex, StringBuilder sb) { if (listIndex > list.size()) return ; if (listIndex == list.size()) { result.add(sb.toString()); return ; } char [] currentCharArray = list.get(listIndex); for (int i = 0 ; i < currentCharArray.length; i++) { sb.append(currentCharArray[i]); backTracking(list, listIndex + 1 , sb); sb.setLength(sb.length() - 1 ); } } }
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
1 2 3 4 5 6 输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。
示例 2:
1 2 输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
1 2 输入: candidates = [2], target = 1 输出: []
提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates 的所有元素 互不相同 1 <= target <= 40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { List<List<Integer>> result = new ArrayList <>(); public List<List<Integer>> combinationSum (int [] candidates, int target) { List<Integer> tempList = new ArrayList <>(); Arrays.sort(candidates); int startIndex = 0 ; backtrack(candidates, startIndex, tempList, 0 , target); return result; } private void backtrack (int [] candidates, int startIndex, List<Integer> tempList, int tempSum, int target) { if (tempSum == target) { result.add(new ArrayList <>(tempList)); return ; } for (int i = startIndex; i < candidates.length; i++) { if (tempSum + candidates[i] > target) { break ; } tempList.add(candidates[i]); backtrack(candidates, i, tempList, tempSum + candidates[i], target); tempList.remove(tempList.size() - 1 ); } } }
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
1 2 输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { List<String> result = new ArrayList <>(); public List<String> generateParenthesis (int n) { dfs("" , n, n); return result; } private void dfs (String s, int leftNum, int rightNum) { if (leftNum > rightNum) { return ; } if (leftNum == 0 && rightNum == 0 ) { result.add(s); return ; } if (leftNum > 0 ) { dfs(s + "(" , leftNum - 1 , rightNum); } if (rightNum > 0 ) { dfs(s + ")" , leftNum, rightNum - 1 ); } } }
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
1 2 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true
示例 2:
1 2 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE" 输出:true
示例 3:
1 2 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB" 输出:false
提示:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15board 和 word 仅由大小写英文字母组成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution { private int [] position = new int [] {-1 , 0 , 1 , 0 , -1 }; public boolean exist (char [][] board, String word) { int rows = board.length; int cols = board[0 ].length; boolean [][] visited = new boolean [rows][cols]; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (board[row][col] == word.charAt(0 )) { if (dfs(board, row, col, visited, 0 , word)) { return true ; } } } } return false ; } private boolean dfs (char [][] board, int row, int col, boolean [][] visited, int index, String word) { if (index == word.length() - 1 ) { return true ; } visited[row][col] = true ; for (int k = 0 ; k < 4 ; k++) { int m = row + position[k]; int n = col + position[k+1 ]; if (m >= 0 && m < board.length && n >= 0 && n < board[0 ].length && !visited[m][n] && board[m][n] == word.charAt(index+1 )) { if (dfs(board, m, n, visited, index + 1 , word)) { return true ; } } } visited[row][col] = false ; return false ; } }
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
示例 1:
1 2 输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]
示例 2:
提示:
1 <= s.length <= 16s 仅由小写英文字母组成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { List<List<String>> result = new ArrayList <>(); public List<List<String>> partition (String s) { List<String> tempList = new ArrayList <>(); backTracking(s, 0 , tempList); return result; } private void backTracking (String s, int startIndex, List<String> tempList) { if (startIndex == s.length()) { result.add(new ArrayList <>(tempList)); return ; } for (int i = startIndex; i < s.length(); i++) { if (isPalindrome(s, startIndex, i)) { tempList.add(s.substring(startIndex, i + 1 )); backTracking(s, i + 1 , tempList); tempList.remove(tempList.size() - 1 ); } } } private boolean isPalindrome (String s, int left, int right) { while (left <= right) { if (s.charAt(left++) != s.charAt(right--)) { return false ; } } return true ; } }
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
1 2 3 输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 class Solution { private List<List<String>> result = new ArrayList <>(); public List<List<String>> solveNQueens (int n) { char [][] board = new char [n][n]; for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n; j++) { board[i][j] = '.' ; } } backTracking(board, 0 , n); return result; } private void backTracking (char [][] board, int row, int n) { if (row == n) { List<String> tempResult = new ArrayList <>(); Arrays.stream(board).forEach(a -> { tempResult.add(new String (a)); }); result.add(tempResult); return ; } for (int col = 0 ; col < n; col++) { if (isValid(board, row, col, n)) { board[row][col] = 'Q' ; backTracking(board, row + 1 , n); board[row][col] = '.' ; } } } private boolean isValid (char [][] board, int row, int col, int n) { for (int i = 0 ; i < n; i++) { if (board[i][col] == 'Q' ) { return false ; } } for (int i = row-1 , j = col-1 ; i >= 0 && j >= 0 ; i--,j--) { if (board[i][j] == 'Q' ) { return false ; } } for (int i = row-1 , j = col + 1 ; i>=0 &&j<n; i--,j++) { if (board[i][j] == 'Q' ) { return false ; } } return true ; } }
图论 给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
1 2 3 4 5 6 7 输入:grid = [ ["1","1","1","1","0"], ["1","1","0","1","0"], ["1","1","0","0","0"], ["0","0","0","0","0"] ] 输出:1
示例 2:
1 2 3 4 5 6 7 输入:grid = [ ["1","1","0","0","0"], ["1","1","0","0","0"], ["0","0","1","0","0"], ["0","0","0","1","1"] ] 输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j] 的值为 '0' 或 '1'
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { private int [] position = {-1 , 0 , 1 , 0 , -1 }; public int numIslands (char [][] grid) { int islandCount = 0 ; int rows = grid.length; int cols = grid[0 ].length; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (grid[row][col] == '1' ) { islandCount++; dfs(grid, row, col); } } } return islandCount; } private void dfs (char [][] grid, int row, int col) { if (grid[row][col] == '0' ) return ; grid[row][col] = '0' ; for (int k = 0 ; k < 4 ; k++) { int m = row + position[k]; int n = col + position[k+1 ]; if (m >= 0 && m < grid.length && n >= 0 && n < grid[0 ].length && grid[m][n] == '1' ) { dfs(grid, m, n); } } } }
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
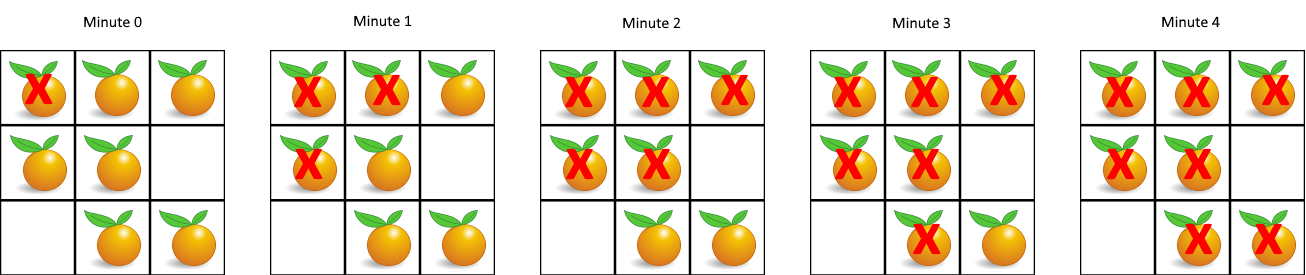
示例 1:
1 2 输入:grid = [[2,1,1],[1,1,0],[0,1,1]] 输出:4
示例 2:
1 2 3 输入:grid = [[2,1,1],[0,1,1],[1,0,1]] 输出:-1 解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
示例 3:
1 2 3 输入:grid = [[0,2]] 输出:0 解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j] 仅为 0、1 或 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 class Solution { private int [] position = {-1 , 0 , 1 , 0 , -1 }; public int orangesRotting (int [][] grid) { int rows = grid.length; int cols = grid[0 ].length; LinkedList<List<Integer>> queue = new LinkedList <>(); int count = 0 ; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (grid[row][col] == 2 ) { dfs(grid, row, col, queue); } } } while (!queue.isEmpty()) { count++; int currentSize = queue.size(); List<List<Integer>> tempList = new ArrayList <>(); for (int i = 0 ; i < currentSize; i++) { List<Integer> tempLocation = queue.pollFirst(); grid[tempLocation.get(0 )][tempLocation.get(1 )] = 2 ; tempList.add(tempLocation); } for (int i = 0 ; i < currentSize; i++) { dfs(grid, tempList.get(i).get(0 ), tempList.get(i).get(1 ), queue); } } for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (grid[row][col] == 1 ) { return -1 ; } } } return count; } private void dfs (int [][] grid, int row, int col, LinkedList<List<Integer>> queue) { for (int k = 0 ; k < 4 ; k++) { int nextI = row + position[k]; int nextJ = col + position[k+1 ]; if (nextI >=0 && nextI < grid.length && nextJ >= 0 && nextJ < grid[0 ].length) { if (grid[nextI][nextJ] == 1 ) { queue.addLast(List.of(nextI, nextJ)); } } } } }
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
1 2 3 输入:numCourses = 2, prerequisites = [[1,0]] 输出:true 解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
1 2 3 输入:numCourses = 2, prerequisites = [[1,0],[0,1]] 输出:false 解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= 5000prerequisites[i].length == 20 <= ai, bi < numCoursesprerequisites[i] 中的所有课程对 互不相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution { public boolean canFinish (int numCourses, int [][] prerequisites) { Map<Integer, List<Integer>> hashMap = new HashMap <>(); int [] degreeArray = new int [numCourses]; for (int [] array : prerequisites) { degreeArray[array[0 ]]++; List<Integer> tempList = hashMap.getOrDefault(array[1 ], new ArrayList <Integer>()); tempList.add(array[0 ]); hashMap.put(array[1 ], tempList); } LinkedList<Integer> queue = new LinkedList <>(); for (int i = 0 ; i < degreeArray.length; i++) { if (degreeArray[i] == 0 ) { queue.addLast(i); numCourses--; } } while (!queue.isEmpty()) { int preCourse = queue.pollFirst(); List<Integer> tempList = hashMap.get(preCourse); if (tempList != null && tempList.size() > 0 ) { for (Integer nextNum : tempList) { degreeArray[nextNum]--; if (degreeArray[nextNum] == 0 ) { queue.addLast(nextNum); numCourses--; } } } } return numCourses == 0 ; } }
**Trie **(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。void insert(String word) 向前缀树中插入字符串 word 。boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 输入 ["Trie", "insert", "search", "search", "startsWith", "insert", "search"] [[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]] 输出 [null, null, true, false, true, null, true] 解释 Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // 返回 True trie.search("app"); // 返回 False trie.startsWith("app"); // 返回 True trie.insert("app"); trie.search("app"); // 返回 True
提示:
1 <= word.length, prefix.length <= 2000word 和 prefix 仅由小写英文字母组成insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 class Trie { TrieNode root = null ; public Trie () { root = new TrieNode (); } public void insert (String word) { TrieNode temp = root; for (int i = 0 ; i < word.length(); i++) { if (temp.childNode[word.charAt(i) - 'a' ] == null ) { temp.childNode[word.charAt(i) - 'a' ] = new TrieNode (); } temp = temp.childNode[word.charAt(i) - 'a' ]; } temp.isVal = true ; } public boolean search (String word) { TrieNode temp = root; for (int i = 0 ; i < word.length(); i++) { if (temp == null ) { break ; } temp = temp.childNode[word.charAt(i) - 'a' ]; } return temp != null ? temp.isVal : false ; } public boolean startsWith (String prefix) { TrieNode temp = root; for (int i = 0 ; i < prefix.length(); i++) { if (temp == null ) { break ; } temp = temp.childNode[prefix.charAt(i) - 'a' ]; } return temp != null ; } class TrieNode { TrieNode[] childNode = new TrieNode [26 ]; boolean isVal; TrieNode() { isVal = false ; } } }
二叉树 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
1 2 输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
示例 3:
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 import java.util.ArrayList;class Solution { private List<Integer> result = new ArrayList <>(); public List<Integer> inorderTraversal (TreeNode root) { start(root); return result; } private void start (TreeNode root) { if (root == null ) { return ; } start(root.left); result.add(root.val); start(root.right); } }
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
1 2 输入:root = [3,9,20,null,null,15,7] 输出:3
示例 2:
1 2 输入:root = [1,null,2] 输出:2
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public int maxDepth (TreeNode root) { return root != null ? 1 + Math.max(maxDepth(root.left), maxDepth(root.right)) : 0 ; } }
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
1 2 输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
示例 2:
1 2 输入:root = [2,1,3] 输出:[2,3,1]
示例 3:
提示:
树中节点数目范围在 [0, 100] 内
-100 <= Node.val <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution { public TreeNode invertTree (TreeNode root) { if (root == null ) return null ; TreeNode temp = root.left; root.left = root.right; root.right = temp; invertTree(root.left); invertTree(root.right); return root; } }
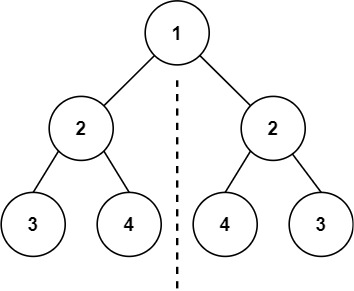
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
1 2 输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
1 2 输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { public boolean isSymmetric (TreeNode root) { return root == null ? true : isSymmetric(root.left, root.right); } private boolean isSymmetric (TreeNode left, TreeNode right) { if (left == null && right == null ) { return true ; } if (left == null || right == null ) { return false ; } if (left.val != right.val) { return false ; } return isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left); } }
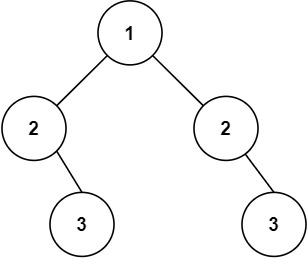
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
1 2 3 输入:root = [1,2,3,4,5] 输出:3 解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
提示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { private int diameter = 0 ; public int diameterOfBinaryTree (TreeNode root) { helper(root); return diameter; } private int helper (TreeNode root) { if (root == null ) { return 0 ; } int left = helper(root.left); int right = helper(root.right); diameter = Math.max(diameter, left + right); return 1 + Math.max(left, right); } }
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
1 2 输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
示例 3:
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 import java.util.ArrayList;import java.util.LinkedList;class Solution { public List<List<Integer>> levelOrder (TreeNode root) { List<List<Integer>> result = new ArrayList <>(); if (root == null ) return result; LinkedList<TreeNode> queue = new LinkedList <TreeNode>(); queue.add(root); int count = queue.size(); while (!queue.isEmpty()) { int currentSize = count; count = 0 ; List<Integer> tempResult = new ArrayList <>(); for (int i = 0 ; i < currentSize; i++) { TreeNode node = queue.pollFirst(); tempResult.add(node.val); if (node.left != null ) { queue.offerLast(node.left); count++; } if (node.right != null ) { queue.offerLast(node.right); count++; } } result.add(tempResult); } return result; } }
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。
示例 1:
1 2 3 输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:
示例 2:
1 2 3 输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums 按 严格递增 顺序排列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { public TreeNode sortedArrayToBST (int [] nums) { return build(nums, 0 , nums.length - 1 ); } private TreeNode build (int [] nums, int startIndex, int endIndex) { if (startIndex > endIndex) return null ; int midIndex = startIndex + (endIndex - startIndex) / 2 ; TreeNode root = new TreeNode (nums[midIndex]); root.left = build(nums, startIndex, midIndex - 1 ); root.right = build(nums, midIndex + 1 , endIndex); return root; } }
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左
子树
只包含
小于
当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
1 2 输入:root = [2,1,3] 输出:true
示例 2:
1 2 3 输入:root = [5,1,4,null,null,3,6] 输出:false 解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { boolean flag = false ; int preNum = 0 ; public boolean isValidBST (TreeNode root) { if (root == null ) return true ; boolean left = isValidBST(root.left); if (!flag) { flag = true ; preNum = root.val; } else { if (root.val <= preNum) { return false ; } preNum = root.val; } boolean right = isValidBST(root.right); return left && right; } }
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)。
示例 1:
1 2 输入:root = [3,1,4,null,2], k = 1 输出:1
示例 2:
1 2 输入:root = [5,3,6,2,4,null,null,1], k = 3 输出:3
提示:
树中的节点数为 n 。
1 <= k <= n <= 1040 <= Node.val <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 import java.util.HashSet;class Solution { private int num; private int currentK; public int kthSmallest (TreeNode root, int k) { currentK = k; helper(root, k); return num; } private void helper (TreeNode root, int k) { if (root == null ) return ; helper(root.left, k); currentK--; if (currentK == 0 ) { num = root.val; } helper(root.right, k); } }
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
1 2 输入: [1,2,3,null,5,null,4] 输出: [1,3,4]
示例 2:
1 2 输入: [1,null,3] 输出: [1,3]
示例 3:
提示:
二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 import java.util.ArrayList;import java.util.LinkedList;class Solution { public List<Integer> rightSideView (TreeNode root) { List<Integer> result = new ArrayList <>(); if (root == null ) return result; LinkedList<TreeNode> queue = new LinkedList <TreeNode>(); queue.add(root); int count = queue.size(); while (!queue.isEmpty()) { int currentSize = count; count = 0 ; for (int i = 0 ; i < currentSize; i++) { TreeNode node = queue.pollFirst(); if (i == currentSize - 1 ) { result.add(node.val); } if (node.left != null ) { queue.offerLast(node.left); count++; } if (node.right != null ) { queue.offerLast(node.right); count++; } } } return result; } }
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历
示例 1:
1 2 输入:root = [1,2,5,3,4,null,6] 输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
示例 3:
提示:
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class Solution { public void flatten (TreeNode root) { if (root == null ) return ; TreeNode left = root.left; TreeNode right = root.right; root.left = null ; root.right = null ; TreeNode tempTail = construct(root, left); construct(tempTail, right); } private TreeNode construct (TreeNode preTail, TreeNode bRoot) { if (bRoot == null ) return preTail; preTail.right = bRoot; preTail = preTail.right; TreeNode left = preTail.left; TreeNode right = preTail.right; preTail.left = null ; preTail.right = null ; if (left != null ) { preTail = construct(preTail, left); } if (right != null ) { preTail = construct(preTail, right); } return preTail; } }
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历 , inorder 是同一棵树的中序遍历 ,请构造二叉树并返回其根节点。
示例 1:
1 2 输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]
示例 2:
1 2 输入: preorder = [-1], inorder = [-1] 输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder 和 inorder 均 无重复 元素inorder 均出现在 preorderpreorder 保证 为二叉树的前序遍历序列inorder 保证 为二叉树的中序遍历序列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 import java.util.HashMap;class Solution { public TreeNode buildTree (int [] preorder, int [] inorder) { HashMap<Integer, Integer> inOrderMap = new HashMap <>(); for (int i = 0 ; i < inorder.length; i++) { inOrderMap.put(inorder[i], i); } return buildTree(0 , preorder, inorder, inOrderMap, 0 , inorder.length - 1 ); } private TreeNode buildTree (int rootIndex, int [] preOrder, int [] inOrder, HashMap<Integer, Integer> inOrderMap, int inOrderStartIndex, int inOrderEndIndex) { if (rootIndex < 0 || rootIndex >= preOrder.length || inOrderStartIndex < 0 || inOrderStartIndex >= inOrder.length || inOrderStartIndex > inOrderEndIndex || inOrderEndIndex < 0 || inOrderEndIndex >= inOrder.length) { return null ; } int val = preOrder[rootIndex]; int inOrderIndex = inOrderMap.get(val); int leftLength = inOrderIndex - inOrderStartIndex; TreeNode root = new TreeNode (val); root.left = buildTree(rootIndex+1 , preOrder, inOrder, inOrderMap, inOrderStartIndex, inOrderIndex - 1 ); root.right = buildTree(rootIndex+leftLength + 1 , preOrder, inOrder, inOrderMap, inOrderIndex+1 , inOrderEndIndex); return root; } }
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
1 2 3 输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
提示:
二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109 -1000 <= targetSum <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public int pathSum (TreeNode root, int targetSum) { return root == null ? 0 : getResult(root, targetSum) + pathSum(root.left, targetSum) + pathSum(root.right, targetSum); } private int getResult (TreeNode root, long targetSum) { if (root == null ) { return 0 ; } int count = root.val == targetSum ? 1 : 0 ; count += getResult(root.left, targetSum - root.val); count += getResult(root.right, targetSum - root.val); return count; } }
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科 中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先 )。”
示例 1:
1 2 3 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
1 2 3 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
1 2 输入:root = [1,2], p = 1, q = 2 输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109所有 Node.val 互不相同 。
p != qp 和 q 均存在于给定的二叉树中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution { public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) return root; TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if (left == null ) return right; if (right == null ) return left; return root; } }
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
1 2 3 输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
1 2 3 输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution { int result = Integer.MIN_VALUE; public int maxPathSum (TreeNode root) { helper(root); return result; } private int helper (TreeNode root) { if (root == null ) return 0 ; int left = helper(root.left); int right = helper(root.right); int temp = root.val; if (left > 0 ) temp += left; if (right > 0 ) temp += right; result = Math.max(result, temp); return Math.max(root.val, Math.max(left, right) + root.val); } }
矩阵 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 。
示例 1:
1 2 输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
1 2 输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
方法一:原地算法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class Solution { public void setZeroes (int [][] matrix) { int rows = matrix.length; int cols = matrix[0 ].length; boolean firstRowFlag = false ; boolean firstColFlag = false ; for (int col = 0 ; col < cols; col++) { if (matrix[0 ][col] == 0 ) firstRowFlag = true ; } for (int row = 0 ; row < rows; row++) { if (matrix[row][0 ] == 0 ) firstColFlag = true ; } for (int row = 1 ; row < rows; row++) { for (int col = 1 ; col < cols; col++) { if (matrix[row][col] == 0 ) { matrix[0 ][col] = 0 ; matrix[row][0 ] = 0 ; } } } for (int row = 1 ; row < rows; row++) { if (matrix[row][0 ] == 0 ) { Arrays.fill(matrix[row], 0 ); } } for (int col = 1 ; col < cols; col++) { if (matrix[0 ][col] == 0 ) { for (int row = 0 ; row < rows; row++) { matrix[row][col] = 0 ; } } } if (firstRowFlag) Arrays.fill(matrix[0 ], 0 ); if (firstColFlag) { for (int row = 0 ; row < rows; row++) { matrix[row][0 ] = 0 ; } } } }
方法二 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Solution { public void setZeroes (int [][] matrix) { int rows = matrix.length; int cols = matrix[0 ].length; boolean [] rowFlag = new boolean [rows]; boolean [] colFlag = new boolean [cols]; for (int row = 0 ; row < rows; row++) { for (int col = 0 ; col < cols; col++) { if (matrix[row][col] == 0 ) { rowFlag[row] = true ; colFlag[col] = true ; } } } for (int row = 0 ; row < rows; row++) { if (rowFlag[row]) { for (int col = 0 ; col < cols; col++) { matrix[row][col] = 0 ; } } } for (int col = 0 ; col < cols; col++) { if (colFlag[col]) { for (int row = 0 ; row < rows; row++) { matrix[row][col] = 0 ; } } } } }
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
1 2 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]
示例 2:
1 2 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 10-100 <= matrix[i][j] <= 100
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 class Solution { private List<Integer> result = new ArrayList <>(); public List<Integer> spiralOrder (int [][] matrix) { int rows = matrix.length; int cols = matrix[0 ].length; int upRow = 0 ; int downRow = rows - 1 ; int leftCol = 0 ; int rightCol = cols - 1 ; int curRow = 0 ; int curCol = 0 ; while (true ) { while (curCol <= rightCol) { result.add(matrix[curRow][curCol++]); } upRow++; curRow++; curCol--; if (upRow > downRow) break ; while (curRow <= downRow) { result.add(matrix[curRow++][curCol]); } rightCol--; curCol--; curRow--; if (rightCol < leftCol) break ; while (curCol >= leftCol) { result.add(matrix[curRow][curCol--]); } downRow--; curRow--; curCol++; if (downRow < upRow) break ; while (curRow >= upRow) { result.add(matrix[curRow--][curCol]); } leftCol++; curCol++; curRow++; if (leftCol > rightCol) break ; } return result; } }
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在** 原地 ** 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
1 2 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
1 2 输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public void rotate (int [][] matrix) { int temp = 0 ; int n = matrix.length - 1 ; for (int i = 0 ; i <= n/2 ; i++) { for (int j = i; j < n-i; j++) { temp = matrix[j][n-i]; matrix[j][n-i] = matrix[i][j]; matrix[i][j] = matrix[n-j][i]; matrix[n-j][i] = matrix[n-i][n-j]; matrix[n-i][n-j] = temp; } } } }
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1:
1 2 输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
示例 2:
1 2 输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public boolean searchMatrix (int [][] matrix, int target) { int rows = matrix.length; int cols = matrix[0 ].length; for (int row = 0 ; row < rows; row++) { for (int col = cols - 1 ; col >= 0 ; col--) { if (matrix[row][col] == target) { return true ; } else if (matrix[row][col] < target) { break ; } else { continue ; } } } return false ; } }
普通数组 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
1 2 3 输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
示例 3:
1 2 输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int maxSubArray (int [] nums) { int [] dp = new int [nums.length]; dp[0 ] = nums[0 ]; int result = dp[0 ]; for (int i = 1 ; i < nums.length; i++) { dp[i] = Math.max(nums[i], nums[i] + dp[i-1 ]); result = Math.max(result, dp[i]); } return result; } }
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
1 2 3 输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
1 2 3 输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public int [][] merge(int [][] intervals) { List<List<Integer>> resultList = new ArrayList <>(); Arrays.sort(intervals, (a, b) -> {return a[0 ] == b[0 ] ? a[1 ] - b[1 ] : a[0 ] - b[0 ];}); int left = intervals[0 ][0 ]; int right = intervals[0 ][1 ]; for (int i = 1 ; i < intervals.length; i++) { if (right >= intervals[i][1 ]) { continue ; } if (right >= intervals[i][0 ]) { right = intervals[i][1 ]; continue ; } resultList.add(List.of(left, right)); left = intervals[i][0 ]; right = intervals[i][1 ]; } resultList.add(List.of(left, right)); int [][] result = new int [resultList.size()][2 ]; for (int i = 0 ; i < result.length; i++) { int [] temp = new int [2 ]; temp[0 ] = resultList.get(i).get(0 ); temp[1 ] = resultList.get(i).get(1 ); result[i] = temp; } return result; } }
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
1 2 3 4 5 6 输入: nums = [1,2,3,4,5,6,7], k = 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
1 2 3 4 5 输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
方法一 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution { public void rotate (int [] nums, int k) { k %= nums.length; if (k == 0 ) return ; reverse(nums, 0 , nums.length - 1 ); reverse(nums, 0 , k - 1 ); reverse(nums, k, nums.length - 1 ); } private void reverse (int [] nums, int left, int right) { if (left > right) return ; while (left < right) { int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; left++; right--; } } }
方法二 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 class Solution { public void rotate (int [] nums, int k) { k = k % (nums.length ); if (k == 0 ) { return ; } int slowIndex = -1 ; int fastIndex = -1 ; while (fastIndex < k - 1 ) fastIndex++; while (fastIndex < nums.length - 1 ) { slowIndex++; fastIndex++; } slowIndex++; fastIndex = 0 ; int [] resultNum = new int [nums.length]; for (int i = 0 ; i < resultNum.length; i++) { if (i < k) { resultNum[i] = nums[slowIndex++]; } else { resultNum[i] = nums[fastIndex++]; } } for (int i = 0 ; i < resultNum.length; i++) { nums[i] = resultNum[i]; } } }
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法, 且在 O(n) 时间复杂度内完成此题。
示例 1:
1 2 输入: nums = [1,2,3,4] 输出: [24,12,8,6]
示例 2:
1 2 输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import java.util.Arrays;class Solution { public int [] productExceptSelf(int [] nums) { int [] preMuti = new int [nums.length]; int [] tailMuti = new int [nums.length]; Arrays.fill(preMuti, 1 ); Arrays.fill(tailMuti, 1 ); int [] result = new int [nums.length]; for (int i = 1 ; i < nums.length; i++) { preMuti[i] = preMuti[i-1 ] * nums[i-1 ]; } for (int i = nums.length - 2 ; i >= 0 ; i--) { tailMuti[i] = tailMuti[i+1 ] * nums[i+1 ]; } for (int i = 0 ; i < nums.length; i++) { result[i] = preMuti[i] * tailMuti[i]; } return result; } }
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
1 2 3 输入:nums = [1,2,0] 输出:3 解释:范围 [1,2] 中的数字都在数组中。
示例 2:
1 2 3 输入:nums = [3,4,-1,1] 输出:2 解释:1 在数组中,但 2 没有。
示例 3:
1 2 3 输入:nums = [7,8,9,11,12] 输出:1 解释:最小的正数 1 没有出现。
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 class Solution { public int firstMissingPositive (int [] nums) { for (int i = 0 ; i < nums.length; i++) { if (nums[i] == (i+1 )) { continue ; } else { if (nums[i] <= 0 || nums[i] > nums.length) { continue ; } else { if (nums[nums[i] - 1 ] == nums[i]) { continue ; } swap(nums, i, nums[i] - 1 ); i--; } } } for (int i = 0 ; i < nums.length; i++) { if (nums[i] != i + 1 ) { return i + 1 ; } } return nums.length + 1 ; } private void swap (int [] nums, int a, int b) { int temp = nums[a]; nums[a] = nums[b]; nums[b] = temp; } }
子串 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:
1 2 输入:nums = [1,1,1], k = 2 输出:2
示例 2:
1 2 输入:nums = [1,2,3], k = 3 输出:2
提示:
1 <= nums.length <= 2 * 104-1000 <= nums[i] <= 1000-107 <= k <= 107
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 import java.util.HashMap;class Solution { public int subarraySum (int [] nums, int k) { Map<Integer, Integer> preSumFreq = new HashMap <>(); preSumFreq.put(0 , 1 ); int preSum = 0 ; int count = 0 ; for (int num : nums) { preSum += num; if (preSumFreq.containsKey(preSum-k)) { count += preSumFreq.get(preSum-k); } preSumFreq.put(preSum, preSumFreq.getOrDefault(preSum, 0 ) + 1 ); } return count; } }
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
示例 2:
1 2 输入:nums = [1], k = 1 输出:[1]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 import java.util.Deque;import java.util.LinkedList;class Solution { public int [] maxSlidingWindow(int [] nums, int k) { int [] ans = new int [nums.length - k + 1 ]; Deque<Integer> queue = new LinkedList <>(); for (int i = 0 ; i < k; i++) { while (!queue.isEmpty() && queue.peekLast() < nums[i]) { queue.removeLast(); } queue.addLast(nums[i]); } ans[0 ] = queue.peekFirst(); for (int i = k; i < nums.length; i++) { if (queue.peekFirst() == nums[i-k]) { queue.removeFirst(); } while (!queue.isEmpty() && queue.peekLast() < nums[i]) { queue.removeLast(); } queue.addLast(nums[i]); ans[i-k+1 ] = queue.peekFirst(); } return ans; } }
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
1 2 3 输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2:
1 2 3 输入:s = "a", t = "a" 输出:"a" 解释:整个字符串 s 是最小覆盖子串。
示例 3:
1 2 3 4 输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
提示:
m == s.lengthn == t.length1 <= m, n <= 105s 和 t 由英文字母组成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class Solution { public String minWindow (String s, String t) { Map<Character, Integer> hashMap = new HashMap <>(); for (char c : t.toCharArray()) hashMap.put(c, hashMap.getOrDefault(c, 0 ) + 1 ); int keySize = hashMap.size(); int countKey = 0 ; int resultLeftIndex = -1 ; int resultLength = s.length() + 1 ; int left = 0 ; for (int right = 0 ; right < s.length(); right++) { char c = s.charAt(right); if (hashMap.containsKey(c)) { hashMap.put(c, hashMap.get(c) - 1 ); if (hashMap.get(c) == 0 ) countKey++; } while (countKey == keySize) { if (right - left + 1 < resultLength) { resultLeftIndex = left; resultLength = right - left + 1 ; } char leftC = s.charAt(left); if (hashMap.containsKey(leftC)) { hashMap.put(leftC, hashMap.get(leftC) + 1 ); if (hashMap.get(leftC) == 1 ) countKey--; } left++; } } return resultLength == s.length() + 1 ? "" : s.substring(resultLeftIndex, resultLeftIndex + resultLength); } }
滑动窗口 给定一个字符串s,请你找出其中不含有重复字符的最长子串 的长度。
示例 1:
1 2 3 输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
1 2 3 输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
1 2 3 4 输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s 由英文字母、数字、符号和空格组成
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution { public int lengthOfLongestSubstring (String s) { Map<Character, Integer> hashMap = new HashMap <>(); int left = 0 ; int result = 0 ; for (int right = 0 ; right < s.length(); right++) { char c = s.charAt(right); if (!hashMap.containsKey(c)) { hashMap.put(c, right); } else { int preIndex = hashMap.get(c) + 1 ; if (preIndex > left) left = preIndex; hashMap.put(c, right); } result = Math.max(result, right - left + 1 ); } return result; } }
给定两个字符串s和p,找到s中所有p的异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
示例 2:
输入: s = “abab”, p = “ab”
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 “ab”, 它是 “ab” 的异位词。
起始索引等于 1 的子串是 “ba”, 它是 “ab” 的异位词。
起始索引等于 2 的子串是 “ab”, 它是 “ab” 的异位词。
提示:
1 <= s.length, p.length <= 3 * 104s 和 p 仅包含小写字母
解法一 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution { public List<Integer> findAnagrams (String s, String p) { List<Integer> result = new ArrayList <>(); int left = 0 ; HashMap<Character, Integer> hashMap = new HashMap <>(); for (int i = 0 ; i < p.length(); i++) { char c = p.charAt(i); hashMap.put(c, hashMap.getOrDefault(c, 0 ) + 1 ); } int zero = hashMap.size(); int countZero = 0 ; for (int right = 0 ; right < s.length(); right++) { char c = s.charAt(right); if (hashMap.containsKey(c)) { hashMap.put(c, hashMap.get(c) - 1 ); if (hashMap.get(c) == 0 ) countZero++; if (countZero == zero) { result.add(left); } } if (right - left + 1 == p.length()) { char tempC = s.charAt(left++); if (hashMap.containsKey(tempC)) { hashMap.put(tempC, hashMap.get(tempC) + 1 ); if (hashMap.get(tempC) == 1 ) countZero--; } } } return result; } }
解法二 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution { public List<Integer> findAnagrams (String s, String p) { List<Integer> result = new ArrayList <>(); char [] pChars = p.toCharArray(); Arrays.sort(pChars); p = new String (pChars); for (int i = 0 ; i + p.length() - 1 < s.length() ; i++) { char [] sChars = s.substring(i, i + p.length()).toCharArray(); Arrays.sort(sChars); if (p.equals(new String (sChars))) { result.add(i); } } return result; } }
双指针 给定一个长度为n的整数数组height。有n条垂线,第 i 条线的两个端点是(i, 0)和(i, height[i]) 。
找出其中的两条线,使得它们与x轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明: 你不能倾斜容器。
示例 1:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
解释: 图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入: height = [1,1]
输出: 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int maxArea (int [] height) { int left = 0 ; int right = height.length - 1 ; int result = 0 ; while (left < right) { result = height[left] < height[right] ? Math.max(result, (right - left) * height[left++]) : Math.max(result, (right - left) * height[right--]); } return result; } }
给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且 j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。
注意: 答案中不可以包含重复的三元组。
示例 1:
输入: nums = [-1,0,1,2,-1,-4]
输出: [[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入: nums = [0,1,1]
输出: []
解释: 唯一可能的三元组和不为 0 。
示例 3:
输入: nums = [0,0,0]
输出: [[0,0,0]]
解释: 唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000105 <= nums[i] <= 105
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Solution { public List<List<Integer>> threeSum (int [] nums) { List<List<Integer>> result = new ArrayList <>(); Arrays.sort(nums); for (int firstIndex = 0 ; firstIndex < nums.length - 2 ; firstIndex++) { if (nums[firstIndex] > 0 ) break ; if (firstIndex > 0 && nums[firstIndex] == nums[firstIndex - 1 ]) continue ; int secondIndex = firstIndex + 1 ; int thirdIndex = nums.length - 1 ; while (secondIndex < thirdIndex) { int sum = nums[firstIndex] + nums[secondIndex] + nums[thirdIndex]; if (sum < 0 ) { while (secondIndex < thirdIndex && nums[secondIndex] == nums[++secondIndex]); } else if (sum > 0 ) { while (secondIndex < thirdIndex && nums[thirdIndex] == nums[--thirdIndex]); } else { result.add(List.of(nums[firstIndex], nums[secondIndex], nums[thirdIndex])); while (secondIndex < thirdIndex && nums[secondIndex] == nums[++secondIndex]); while (secondIndex < thirdIndex && nums[thirdIndex] == nums[--thirdIndex]); } } } return result; } }
给定n个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入: height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
解释: 上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入: height = [4,2,0,3,2,5]
输出: 9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class Solution { public int trap (int [] height) { int max = -1 ; int result = 0 ; LinkedList<Integer> stack = new LinkedList <>(); for (int i = 0 ; i < height.length; i++) { if (max == -1 && height[i] == 0 ) continue ; if (max == -1 ) { max = height[i]; stack.push(height[i]); continue ; } if (height[i] > max) { while (stack.peek() < max) { result += (max - stack.poll()); } stack.poll(); stack.push(height[i]); max = height[i]; continue ; } if (height[i] > stack.peek()) { LinkedList<Integer> queue = new LinkedList <>(); while (height[i] > stack.peek()) { result += (height[i] - stack.poll()); queue.addLast(height[i]); } while (!queue.isEmpty()) stack.push(queue.pollFirst()); } stack.push(height[i]); } return result; } }
给定一个数组nums,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
1 2 输入: nums = [0,1,0,3,12] 输出: [1,3,12,0,0]
示例 2:
提示 :
1 <= nums.length <= 104231 <= nums[i] <= 231 - 1
解法一 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public void moveZeroes (int [] nums) { int left = 0 ; for (int right = 0 ; right < nums.length; right++) { if (nums[right] != 0 ) { int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; left++; } } } }
解法二 1 2 3 4 5 6 7 8 9 10 11 12 13 14 import java.util.Arrays;class Solution { public void moveZeroes (int [] nums) { int [] newNums = new int [nums.length]; int index = 0 ; for (int i = 0 ; i < nums.length; i++) { if (nums[i] != 0 ) newNums[index++] = nums[i]; } for (int i = 0 ; i < nums.length; i++) { nums[i] = newNums[i]; } } }
哈希 给你一个字符串数组,请你将字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的所有字母得到的一个新单词。
示例 1:
1 2 输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"] 输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
1 2 输入: strs = [""] 输出: [[""]]
示例 3:
1 2 输入: strs = ["a"] 输出: [["a"]]
提示:
1 <= strs.length <= 1040 <= strs[i].length <= 100strs[i] 仅包含小写字母
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { public List<List<String>> groupAnagrams (String[] strs) { List<List<String>> result = new ArrayList <>(); HashMap<String, List<String>> hashMap = new HashMap <>(); for (String str : strs) { char [] tempChars = str.toCharArray(); Arrays.sort(tempChars); String tempString = new String (tempChars); List<String> list = hashMap.getOrDefault(tempString, new ArrayList <String>()); list.add(str); hashMap.put(tempString, list); } hashMap.values().forEach(value -> { result.add(value); }); return result; } }
给定一个未排序的整数数组nums,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为O(n)的算法解决此问题。
示例 1:
输入: nums = [100,4,200,1,3,2]
输出: 4
解释: 最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。示例 2:
输入: nums = [0,3,7,2,5,8,4,6,0,1]
输出: 9
提示:
0 <= nums.length <= 105109 <= nums[i] <= 109
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import java.util.HashSet;class Solution { public int longestConsecutive (int [] nums) { HashSet<Integer> hashSet = new HashSet <>(); Arrays.stream(nums).forEach(num -> {hashSet.add(num);}); int result = 0 ; for (int num : nums) { int tempResult = 1 ; int preNum = num - 1 ; int nextNum = num + 1 ; hashSet.remove(num); while (hashSet.contains(preNum)) { tempResult++; hashSet.remove(preNum); preNum--; } while (hashSet.contains(nextNum)) { tempResult++; hashSet.remove(nextNum); nextNum++; } result = Math.max(result, tempResult); } return result; } }
给定一个整数数组nums和一个整数目标值target,请你在该数组中找出和为目标值 target 的那两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入: nums = [2,7,11,15], target = 9
输出: [0,1]
解释: 因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入: nums = [3,2,4], target = 6
输出: [1,2]
示例 3:
输入: nums = [3,3], target = 6
输出: [0,1]
提示:
2 <= nums.length <= 104109 <= nums[i] <= 109109 <= target <= 109只会存在一个有效答案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int [] twoSum(int [] nums, int target) { HashMap<Integer, Integer> hashMap = new HashMap <>(); int [] result = new int [2 ]; for (int i = 0 ; i < nums.length; i++) { if (hashMap.containsKey(target - nums[i])) { result[0 ] = i; result[1 ] = hashMap.get(target - nums[i]); break ; } hashMap.put(nums[i], i); } return result; } }
ps:测试更新时间 2024.09.27